Shankar’s Principles of Quantum Mechanics is a cornerstone text‚ offering comprehensive insights into foundational principles and practical applications․ The second edition enhances clarity and depth‚ making it an invaluable resource for both students and researchers․
1․1 Historical Context and Development of Quantum Mechanics
Quantum mechanics emerged in the early 20th century as a revolutionary response to the limitations of classical physics․ Key figures like Max Planck‚ Albert Einstein‚ and Niels Bohr laid the groundwork by introducing concepts such as quantized energy and wave-particle duality․ The 1920s saw the development of two groundbreaking frameworks: Erwin Schrödinger’s wave mechanics and Werner Heisenberg’s matrix mechanics‚ both aiming to describe the behavior of particles at atomic and subatomic levels․
The Heisenberg Uncertainty Principle‚ formulated in 1927‚ became a cornerstone of quantum theory‚ emphasizing the intrinsic limits of measuring certain pairs of physical properties․ Later‚ Paul Dirac’s work unified quantum mechanics with special relativity‚ while Richard Feynman’s path integral formulation offered a new perspective on quantum processes․ Shankar’s text provides a detailed exploration of these historical milestones‚ highlighting how they collectively shaped the principles of quantum mechanics․
These developments not only resolved long-standing puzzles but also opened new avenues for understanding matter and energy․ Shankar’s book serves as a bridge between the historical roots and modern applications of quantum theory․
1․2 Basic Postulates and Principles of Quantum Mechanics
Quantum mechanics is built on a set of fundamental postulates that define its theoretical framework․ The first postulate states that the state of a physical system is fully described by a wave function‚ which contains all possible information about the system․ The second postulate introduces operators‚ or observables‚ which correspond to measurable quantities like energy and momentum․
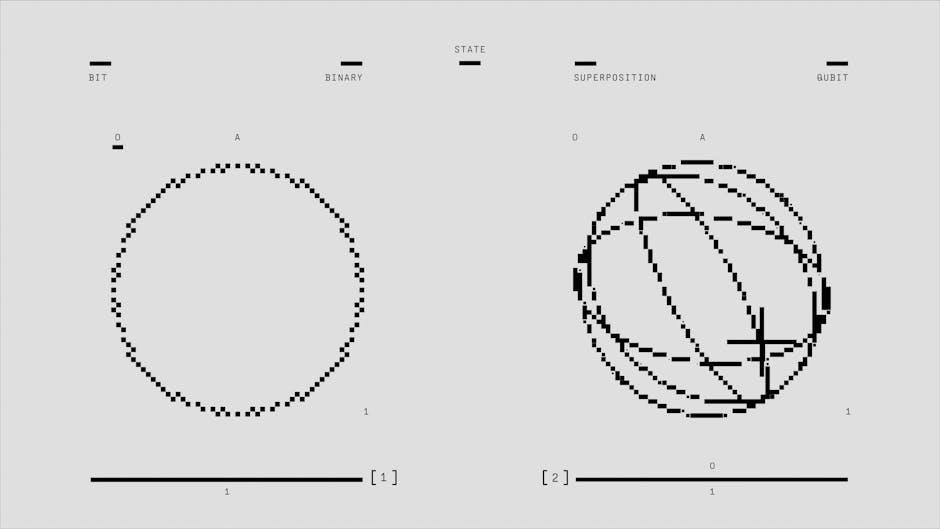
A third postulate establishes the principle of superposition‚ where a system can exist in multiple states simultaneously until measured․ The fourth postulate addresses measurement outcomes‚ linking them to probabilities derived from the wave function․ Additionally‚ the Heisenberg Uncertainty Principle underscores the inherent limitations in simultaneously knowing certain pairs of quantities‚ such as position and momentum․
These principles‚ as explained in Shankar’s text‚ form the backbone of quantum theory‚ providing a consistent and coherent explanation for phenomena at the atomic and subatomic level․ They emphasize the probabilistic nature of quantum systems and the role of observation in determining outcomes․
1․3 The Role of Shankar’s Book in Teaching Quantum Mechanics
R․ Shankar’s Principles of Quantum Mechanics has become a cornerstone in the education of quantum theory‚ particularly for graduate-level students․ The book is widely praised for its clear and accessible presentation of complex concepts‚ making it an essential resource for both students and researchers․ Shankar’s approach emphasizes foundational principles while providing practical insights‚ ensuring a deep understanding of the subject․ The second edition introduces significant updates‚ enhancing the clarity and depth of key concepts‚ making it even more invaluable for modern studies․ Its comprehensive coverage of topics‚ from basic postulates to advanced formulations like path integrals‚ ensures that readers gain a holistic view of quantum mechanics․ The book’s structured approach and detailed explanations have solidified its reputation as a go-to text for mastering quantum theory‚ bridging the gap between theoretical frameworks and practical applications․

Key Principles of Quantum Mechanics
Quantum mechanics is built on core principles like wave functions‚ the Schrödinger equation‚ and the Heisenberg uncertainty principle․ These concepts‚ along with operators and observables‚ form the theoretical framework of the discipline․
2․1 Wave Functions and Their Interpretation
In quantum mechanics‚ wave functions play a central role in describing the quantum state of a system․ The wave function‚ typically denoted by ψ‚ encapsulates all possible information about a particle or system․ Its interpretation‚ primarily through the Copenhagen interpretation‚ suggests that the square of the wave function’s absolute value‚ |ψ|²‚ represents the probability density of finding the particle in a specific state or position․ Wave functions exist in a multidimensional space known as Hilbert space‚ distinguishing quantum mechanics from classical physics․ The normalization of wave functions ensures that the total probability of all possible states equals one‚ maintaining consistency in probabilistic outcomes․ The time-dependent and time-independent Schrödinger equations govern the evolution of wave functions‚ with the latter describing stationary states where probability densities remain constant over time․ Additionally‚ the Heisenberg Uncertainty Principle is inherently linked to wave functions‚ as they mathematically impose limits on simultaneous knowledge of position and momentum․ Thus‚ wave functions are fundamental to understanding quantum phenomena‚ bridging mathematics and physical interpretation․
2․2 The Schrödinger Equation and Its Significance
The Schrödinger equation is a cornerstone of quantum mechanics‚ describing how quantum states evolve over time․ It is a partial differential equation that relates the wave function of a system to its energy‚ both kinetic and potential․ The time-dependent Schrödinger equation governs non-stationary states‚ while the time-independent version applies to stationary states‚ where energy is conserved․ The equation is foundational for calculating wave functions‚ which encode all information about a quantum system․ Solutions to the Schrödinger equation yield probability amplitudes‚ enabling predictions of measurable quantities like energy levels and transition probabilities․ Its significance lies in its ability to predict experimental results with remarkable accuracy‚ from atomic spectra to semiconductor behavior․ In Shankar’s book‚ the Schrödinger equation is extensively used to derive key results‚ such as the energy levels of the hydrogen atom and the scattering cross-sections in quantum systems․ This equation is central to understanding quantum phenomena and remains a fundamental tool in modern physics research․
2․3 The Heisenberg Uncertainty Principle
The Heisenberg Uncertainty Principle is a foundational concept in quantum mechanics‚ asserting that certain pairs of physical properties‚ such as position and momentum‚ cannot be simultaneously measured with arbitrary precision․ This principle‚ formulated by Werner Heisenberg‚ arises from the inherent limitations of quantum systems and the nature of wave functions․ It fundamentally challenges classical notions of determinism‚ introducing an unavoidable “fuzziness” in the description of subatomic particles․ The uncertainty principle has profound implications for understanding quantum phenomena‚ such as the behavior of electrons in atoms and the probabilistic nature of particle interactions․ In Shankar’s text‚ this principle is explored in depth‚ connecting it to the mathematical framework of quantum mechanics and its experimental verifications․ The principle underscores the non-intuitive nature of quantum systems and remains a cornerstone of modern physics‚ influencing fields from quantum computing to high-energy physics․
2․4 Operators and Observables in Quantum Mechanics
In quantum mechanics‚ operators play a central role in describing physical observables‚ such as position‚ momentum‚ energy‚ and angular momentum․ These operators act on wave functions‚ producing eigenvalues that correspond to measurable quantities․ Observables are the dynamic variables of a system‚ and their corresponding operators must satisfy specific mathematical properties‚ such as Hermiticity‚ to ensure real eigenvalues․ Shankar’s text provides a detailed explanation of how operators are constructed and their relationship to observables․ The principle of associating observables with linear operators is a cornerstone of quantum theory‚ enabling the formulation of expectation values and measurement probabilities․ Operators also encode the symmetries of a system‚ linking them to conserved quantities․ Understanding operators and observables is essential for solving quantum mechanics problems‚ as they form the bridge between theoretical formalism and experimental outcomes․ Shankar’s approach clarifies these concepts‚ making them accessible for advanced students and researchers․

Specific Topics Covered in Shankar’s Book
Shankar’s book covers a wide range of topics‚ including the path integral formulation‚ angular momentum quantization‚ the hydrogen atom‚ perturbation theory‚ and scattering theory․ These chapters provide in-depth analysis and practical applications of quantum mechanics principles․
3․1 The Path Integral Formulation of Quantum Mechanics
The path integral formulation‚ introduced by Richard Feynman‚ offers an alternative approach to quantum mechanics‚ complementing the Schrödinger equation․ In Shankar’s book‚ this topic is explored in depth‚ providing a rigorous mathematical framework and intuitive explanations․ The formulation describes quantum transitions as sums over all possible paths‚ weighted by their action‚ offering insights into the probabilistic nature of quantum systems․ Shankar’s presentation emphasizes the importance of this method in understanding phenomena like interference and tunneling‚ while also highlighting its utility in perturbation theory and scattering processes․ The book includes detailed derivations and examples‚ making the concept accessible to graduate students․ This section is particularly valuable for its clarity and its ability to connect abstract principles to practical applications in modern quantum mechanics research․
3․2 Angular Momentum and Its Quantization
Angular momentum‚ a fundamental concept in quantum mechanics‚ is thoroughly explored in Shankar’s book‚ with a focus on its quantization and implications․ The text distinguishes between orbital angular momentum‚ associated with particle motion‚ and spin angular momentum‚ an intrinsic property․ Shankar emphasizes that angular momentum in quantum systems is quantized‚ meaning it can only take specific discrete values․ This quantization arises from the mathematical properties of angular momentum operators and their eigenvalues․ The book provides detailed derivations of angular momentum algebra‚ commutation relations‚ and eigenvalue equations‚ making the abstract concept accessible․ Shankar also discusses the addition of angular momenta and their role in determining quantum states․ Practical examples and exercises illustrate how angular momentum quantization underpins phenomena like electron spin and the structure of atoms․ This section is essential for understanding quantum systems‚ offering a rigorous yet clear presentation of angular momentum’s role in modern quantum theory․
3․3 The Hydrogen Atom and Energy Levels
The hydrogen atom‚ as the simplest atomic system‚ plays a pivotal role in understanding quantum mechanics․ In Shankar’s Principles of Quantum Mechanics‚ the analysis of the hydrogen atom reveals the quantized nature of energy levels‚ governed by the Schrödinger equation․ The equation is solved by separating it into radial and angular components‚ leading to wave functions characterized by quantum numbers: the principal quantum number ( n )‚ the azimuthal quantum number ( l )‚ and the magnetic quantum number ( m_l )․ The energy levels depend solely on ( n )‚ resulting in degeneracy across different ( l ) values for the same ( n )․ This degeneracy arises from the spherical symmetry of the Coulomb potential‚ which influences the radial part of the wave function․ The book elucidates how transitions between these energy levels correspond to the emission and absorption spectra‚ aligning with the Rydberg formula․ Shankar’s treatment provides a foundational understanding of quantum numbers and their role in determining electron configurations‚ essential for both theoretical and practical applications in quantum mechanics․
3․4 Perturbation Theory and Its Applications
Perturbation theory is a powerful tool in quantum mechanics for analyzing systems where the Hamiltonian can be divided into a solvable part and a small perturbation․ In Shankar’s Principles of Quantum Mechanics‚ this method is extensively explored‚ enabling approximate solutions to complex problems․ The book discusses both time-independent and time-dependent perturbation theories․ Time-independent perturbation theory is used when the perturbation is static‚ while time-dependent perturbation theory handles cases where the perturbation varies with time‚ such as in interactions with electromagnetic fields․ Shankar provides detailed derivations of energy shifts and transition probabilities‚ illustrating how perturbation theory applies to real-world phenomena like the Zeeman effect and the Stark effect․ The text also emphasizes the importance of mathematically rigorous formulations‚ such as the perturbing Hamiltonian and the computation of corrections to energy levels and wave functions․ These concepts are crucial for understanding quantum systems beyond exactly solvable models‚ making perturbation theory a cornerstone of modern quantum mechanics research and applications․
3․5 Scattering Theory and Cross-Section Analysis
Scattering theory is a fundamental area of quantum mechanics that examines how particles interact and scatter off potentials or other particles․ In Shankar’s Principles of Quantum Mechanics‚ this topic is explored in depth‚ providing a rigorous mathematical framework․ The concept of the scattering cross-section is central‚ quantifying the probability of particles scattering at specific angles or energies․ Shankar discusses both time-dependent and time-independent approaches to scattering‚ emphasizing the importance of the scattering amplitude and its relation to the cross-section․ The Born approximation is introduced as a simplifying tool for weak potentials‚ allowing for approximate solutions․ Additionally‚ the text covers partial wave analysis‚ which decomposes the scattering process into angular momentum components‚ and its application to spherically symmetric potentials․ These methods are essential for understanding phenomena in nuclear and particle physics‚ making scattering theory a vital tool for researchers and students alike․ Shankar’s treatment ensures a clear and comprehensive understanding of this critical area․

Problem Solving and Calculations
This section focuses on problem-solving strategies in quantum mechanics‚ detailing key calculations and the role of Gaussian processes in quantum diffusion․ It aids students and researchers in analyzing quantum systems effectively․
4․1 Strategies for Solving Quantum Mechanics Problems
Shankar’s textbook provides a systematic approach to solving quantum mechanics problems‚ emphasizing the use of postulates and principles․ Key strategies include interpreting wave functions‚ applying operators‚ and solving Schrödinger equations․ The book highlights the importance of understanding uncertainty principles and angular momentum quantization․ Practical examples‚ such as calculating energy levels and analyzing scattering processes‚ are presented with clarity․ Gaussian processes and diffusion models are introduced to tackle complex quantum systems․ The second edition enhances problem-solving techniques‚ offering updated methodologies and improved explanations․ Readers are encouraged to engage with derivations and exercises to solidify their understanding․ This structured approach ensures that students can systematically address a wide range of quantum mechanics problems‚ from foundational concepts to advanced applications․
4․2 Examples of Key Calculations in Shankar’s Book
Shankar’s text provides detailed examples of key quantum mechanics calculations‚ such as solving the Schrödinger equation for free particles and analyzing the hydrogen atom’s energy levels․ The book includes derivations of angular momentum quantization and applications of perturbation theory․ Readers are guided through calculations involving Gaussian processes for quantum diffusion and scattering cross-section analysis․ These examples are supported by clear mathematical steps and physical interpretations․ The second edition enhances these calculations with updated derivations and numerical methods․ Shankar’s approach ensures that students can follow complex computations‚ such as solving Schrödinger equations for various potentials and understanding operator applications․ These examples are essential for mastering quantum mechanics and are presented in a way that bridges theoretical concepts with practical problem-solving․
4․3 The Role of Gaussian Processes in Quantum Diffusion
Gaussian processes play a significant role in quantum diffusion‚ particularly in calculating rates and understanding the interplay between quantum and classical systems․ These processes are utilized to model stochastic dynamics in quantum mechanics‚ providing a framework for analyzing diffusion phenomena․ Shankar’s book explores how Gaussian processes are applied to solve quantum diffusion problems‚ such as the spreading of wave packets and the behavior of free particles․ The text highlights the importance of Gaussian distributions in describing probability amplitudes and their time evolution․ Additionally‚ the book connects Gaussian processes to operator formalisms and path integral methods‚ offering a comprehensive view of their role in quantum systems․ This section is particularly valuable for understanding the mathematical tools used in modern quantum mechanics research and their practical applications in solving complex problems․
4;4 Solving Schrödinger Equations for Free Particles
Solving the Schrödinger equation for free particles is a fundamental exercise in quantum mechanics‚ as it provides insights into the behavior of particles in the absence of external potentials․ In Shankar’s book‚ this topic is addressed with clarity‚ offering detailed derivations and examples․ The free particle Schrödinger equation is solved using separation of variables‚ leading to plane wave solutions․ These solutions describe the wave function of a particle with definite momentum and energy․ The time-dependent Schrödinger equation is also explored‚ revealing how wave packets evolve over time․ Shankar emphasizes the importance of boundary conditions and normalization in obtaining physically meaningful solutions․ Additionally‚ the book discusses the concept of wave function spreading‚ a hallmark of quantum mechanics‚ and its implications for particle localization․ This section is essential for understanding the dynamics of quantum systems and serves as a foundation for more complex problems in quantum mechanics․

The Second Edition of Shankar’s Book
The second edition of Shankar’s Principles of Quantum Mechanics introduces significant updates and improvements․ It enhances clarity‚ expands on key concepts‚ and incorporates modern developments‚ making it a vital resource for contemporary quantum mechanics studies․
5․1 Major Additions and Updates in the Second Edition
The second edition of Principles of Quantum Mechanics by Ramamurti Shankar features numerous enhancements․ Key updates include improved explanations of foundational concepts‚ expanded discussions on modern topics‚ and additional problem sets․ Shankar has also incorporated new sections on emerging areas of quantum mechanics‚ ensuring the text remains relevant to contemporary research and teaching․ The clarity of presentations has been refined‚ making complex ideas more accessible to students and researchers alike․ Furthermore‚ the second edition addresses feedback from the academic community‚ introducing streamlined derivations and more intuitive examples․ These updates ensure that the book continues to serve as a comprehensive and authoritative resource for graduate-level quantum mechanics studies․
5․2 Enhanced Clarity and Presentation of Key Concepts
The second edition of Principles of Quantum Mechanics by Ramamurti Shankar is notable for its enhanced clarity and improved presentation of key concepts․ Shankar has refined the explanations of complex topics‚ such as wave functions‚ operators‚ and the Heisenberg uncertainty principle‚ making them more accessible to readers․ The text now includes more intuitive examples and streamlined derivations‚ which aid in understanding abstract ideas․ Additionally‚ the organization of chapters has been optimized to provide a logical flow of concepts‚ from foundational principles to advanced applications․ The improved presentation ensures that students and researchers can grasp intricate quantum mechanics ideas with greater ease․ Shankar’s emphasis on clarity makes the book an indispensable resource for both learning and reference‚ solidifying its reputation as a leading text in the field of quantum mechanics․
5․3 Relevance of the Second Edition for Modern Studies

The second edition of Principles of Quantum Mechanics remains highly relevant for modern studies in quantum physics․ It incorporates updated discussions on contemporary topics‚ ensuring alignment with current research and educational needs․ Shankar’s revisions reflect advancements in the field‚ making the text a valuable resource for both students and researchers․ The book’s emphasis on foundational principles‚ such as the Schrödinger equation and perturbation theory‚ provides a solid framework for understanding modern applications in quantum computing‚ materials science‚ and particle physics․ Additionally‚ the inclusion of new problem sets and examples facilitates practical learning‚ preparing students for cutting-edge research․ The second edition’s comprehensive approach ensures its continued importance in shaping the understanding of quantum mechanics for future generations of physicists․ Its relevance is underscored by its widespread adoption in graduate programs and its use as a reference by professionals in the field․
Principles of Quantum Mechanics by Shankar stands as a foundational text‚ offering profound insights and comprehensive coverage of quantum theory․ Its clarity and depth make it an essential resource for students‚ researchers‚ and professionals alike․
6․1 The Impact of Shankar’s Work on Quantum Mechanics
R․ Shankar’s Principles of Quantum Mechanics has profoundly influenced the field of quantum mechanics‚ serving as a cornerstone for education and research․ Its comprehensive approach and clarity have made complex concepts accessible to students and professionals alike․ The book’s emphasis on foundational principles and practical applications has solidified its reputation as a go-to resource in quantum theory․ Shankar’s work has also inspired further exploration and advancements in the field‚ particularly through its updated second edition‚ which incorporates modern perspectives and methodologies․ By bridging the gap between theory and application‚ Shankar’s contributions continue to shape the understanding and development of quantum mechanics‚ ensuring its relevance for future generations of physicists and researchers․
6․2 Future Directions in Quantum Mechanics Research
Future research in quantum mechanics is expected to focus on advancing quantum computing‚ exploring quantum information theory‚ and delving deeper into the mysteries of quantum systems․ Innovations in experimental techniques will play a crucial role in testing theoretical predictions and unlocking new phenomena․ The integration of quantum mechanics with other fields‚ such as condensed matter physics and high-energy physics‚ promises to reveal new insights․ Additionally‚ advancements in computational methods and simulations will aid in solving complex quantum problems․ Researchers are also likely to explore the applications of quantum mechanics in real-world scenarios‚ such as quantum cryptography and quantum sensing․ As the field evolves‚ interdisciplinary collaborations will drive innovation‚ ensuring that quantum mechanics remains at the forefront of scientific discovery․ These developments will build on the foundational principles outlined in texts like Shankar’s‚ guiding the next generation of physicists in their pursuit of knowledge․
6․3 The Importance of Shankar’s Book for Students and Researchers

Principles of Quantum Mechanics by Ramamurti Shankar is an indispensable resource for both students and researchers․ Its comprehensive coverage of quantum mechanics provides a solid foundation for understanding the subject․ The book’s clear and concise explanations‚ along with its structured approach‚ make it accessible to learners at various levels․ Researchers appreciate its depth and the inclusion of advanced topics‚ such as perturbation theory and scattering theory‚ which are essential for cutting-edge studies․ The second edition’s updates ensure relevance to modern research and educational needs․ Shankar’s emphasis on problem-solving strategies and key calculations equips students with practical skills‚ while its theoretical rigor appeals to researchers․ This text serves as a bridge between foundational concepts and contemporary advancements‚ making it a vital tool for anyone engaged in quantum mechanics․ Its availability in PDF format further enhances its accessibility‚ ensuring widespread use in academic and research settings․

